An "Iterated Function System" (IFS) is a mathematical description of a large class of fractal shapes. An IFS consists of a set of "maps" (functions that warp space) that explicitly list the self-similarities of the shape.
For example, the Sierpinski triangle, 4-dragon, and fern below are all typical examples of shapes that can be represented as an IFS.


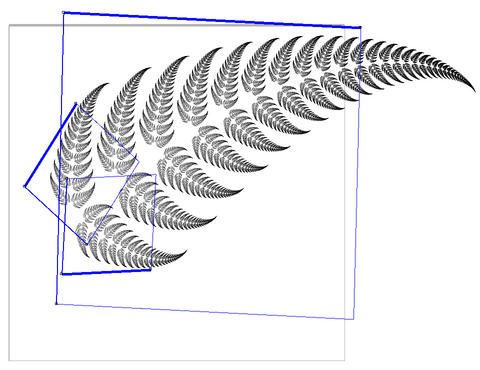
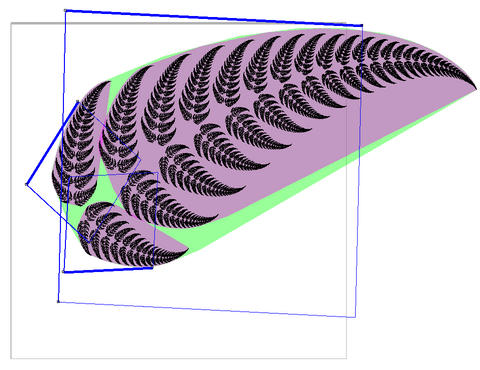
What I present in the program and paper below is a method for computing convex bounding volumes for arbitrary IFS. The method reduces IFS bounding to the well-known problem of convex linear optimization, allowing tight bounding volumes to be produced quickly.
Download my Iterated Function System viewer, including source code and all the IFS's pictured on this page and featured in the paper:
Download a technical paper (PDF) [300 KB] describing the details of how to bound IFS's via convex optimization. This paper has been submitted to the Graphics Interface 2003 conference.
Download a presentation (Powerpoint) [1.3 MB] explaining the basics of IFS's, as well as Rice's work on sphere bounding and my own work on IFS bounds via convex optimization.
Download a 2-minute movie (MPEG) [11 MB] of me showing the basic features of my bounding system in 2D, or a short 3d movie (MPEG) [3 MB].