Timelapse Image Alignment: Alignment
This page describes the actual alignment process.
The input images are first:
- Radiometrically calibrated, which compensates for
lens vignetting and sensor nonlinearity.
- Geometrically calibrated, which compensates for
radial lens distortion.
- Scaled to a uniform brightness, which allows the images
to be compared.
The images are all now nicely linear in brightness and
geometry. They can thus be precicely compared against
one another, which we do on a chip-by-chip basis.
To line up each image with the center image, we use the
standard technique of chip-by-chip correlation. For
overlapping 16x16 pixel portions ("chips") of the unknown
image, we search the center image for the most similar
pixels. If by "most similar" we mean the corresponding chip with
the minimum-sum-of-squared-difference pixel values, we can
do this efficiently using the fast correlation property of
the FFT.
Chip matching is still quite slow, however, so we shrink
both images by a factor of 5 before the search. It still takes
several minutes to establish a match for each chip of the
unknown image. The image-to-image offsets for each match are
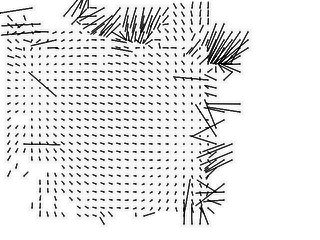
plotted in the leftmost line images below.
Clearly, one significant problem with this approach is
"false correlations"--since about half of the unknown image
isn't even visible in the known image, any image correspondences
in that half are purely due to chance. Worse, uniform
regions of the sky and dark featureless shadows tend not to
match well; so overall a large number of correlations are
meaningless.
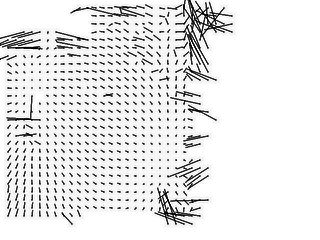
We filter out these bad correlations using a two-step process.
First we pick a bulk offset (in practice, one of the sample
offsets), and discard shifts that are
far from this offset--see the middle line images below.
We then perform a least-squares fit of
the remaining offsets to an arbitrary perspective matrix,
throw out the point with the worst fit, and repeat.
This point removal process may not converge, and all points
will be removed; in this case we pick another offset and
start again. If the offset is good, however, it will converge
on a sizable number of chips that all agree well with a single
perspective mapping, in which case we're done.
We then have a good perspective mapping between the images,
and so can reassemble the two images. We use a few pixels of
edge feathering to hide the seam between the two. See the
results page for examples of the final
correlation.
2002_06_18
2002_07_16
2002_07_25
2002_08_13
2002_08_16
2002_08_22
2002_09_05
2002_09_10
2002_09_16
2002_09_24
2002_10_07
2002_10_18
2002_10_24
2002_10_28
2002_11_01
2002_11_08
2002_11_15
2002_11_25
2002_11_27
2002_12_05
2002_12_06
2002_12_23
2002_12_27
2003_01_09
2003_01_17
2003_01_24
2003_02_19
2003_03_06
2003_03_20
2003_04_10
2003_04_29